Hình tứ diện đều có bao nhiêu mặt phẳng đối xứng, cạnh, trục, tâm đối xứng

Hình tứ diện đều là gì?

Hình tứ diện đều là một trong những khái niệm khá dễ hiểu. Cụ thể, trong không gian cho 4 điểm không đồng phẳng A, B, C, D. Khối đa diện có 4 đỉnh A, B, C, D gọi là khối tứ diện. Nếu những khối tự diện này có các mặt là tam giác đều thì được gọi là khối tứ diện đều.

Nói một cách dễ hiểu nhất thì tứ diện đều là tứ diện có 4 mặt là tam giác đều. Tứ diện đều là một hình chóp tam giác đều và  ngược lại, nếu hình chóp tam giác đều có thêm điều kiện cạnh bên bằng cạnh đáy thì sẽ tạo ra tứ diện đều.

Hình tứ diện đều có bao nhiêu mặt phẳng đối xứng, cạnh, trục, tâm đối xứng?

Tứ diện đều có 4 mặt và 6 cạnh. Cụ thể là:

• 4 mặt tứ diện là (ABC); (ACD); (ABD); (BDC).
• 6 cạnh của tứ diện là AB; AC; AD; BD; BC; CD.
• Trong đó các cạnh bên đều sẽ bằng nhau:  AB = AC = AD = BD = BC = CD.
• Góc ở mỗi mặt tứ diện là 60 độ.

Hình tứ diện đều có 6 mặt đối xứng. Mỗi mặt đều chứa 1 cạnh và trung điểm cạnh đối diện (hình vẽ).

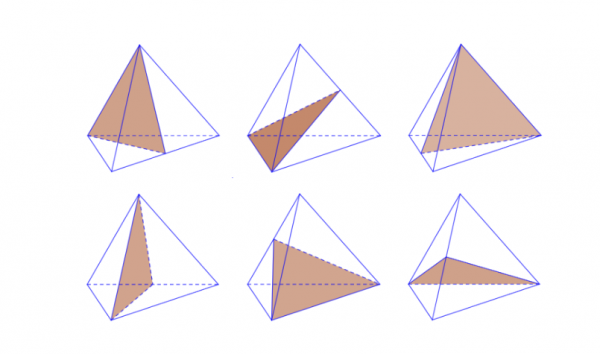
6 mặt đối xứng của hình tứ diện đều

Tứ diện đều có các cặp cạnh đối vuông góc, đoạn nối trung điểm 2 cạnh đối là đoạn vuông góc chung của 2 cạnh đối đó. Và khoảng cách giữa hai cạnh đối diện của tứ diện đều bằng độ dài đoạn thẳng nối hai trung điểm của hai cạnh đối diện ấy.