Bát diện đều có bao nhiêu mặt phẳng đối xứng, đây có lẽ là câu hỏi trong toán học được khá nhiều người quan tâm nhiều nhất hiện nay. Toán học là một trong những môn học quan trọng, đi đối với văn học thì cả hai môn học này chính là hai môn học chính của bất kì những khối lớp nào hiện nay. Từ lớp 1 cho đến lớp 12 thì toán học, văn học chính là hai môn học trọng điểm và quan trọng hơn so với những môn học khác.
Toán học chính là một ngành chuyên nghiên cứu về những con số số, hình học cũng như cấu trúc trong không gian mà bắt buộc ai từ khi sinh ra cũng cần phải học. Vậy thì hôm nay chúng ta cùng nhau tìm hiểu về một trong những vấn đề về hình học trong toán học hiện nay được nhiều bạn tìm hiểu Bát diện đều có bao nhiêu mặt phẳng đối xứng nhé qua bài viết sau đây nhé.
Bát diện đều là hình gì?
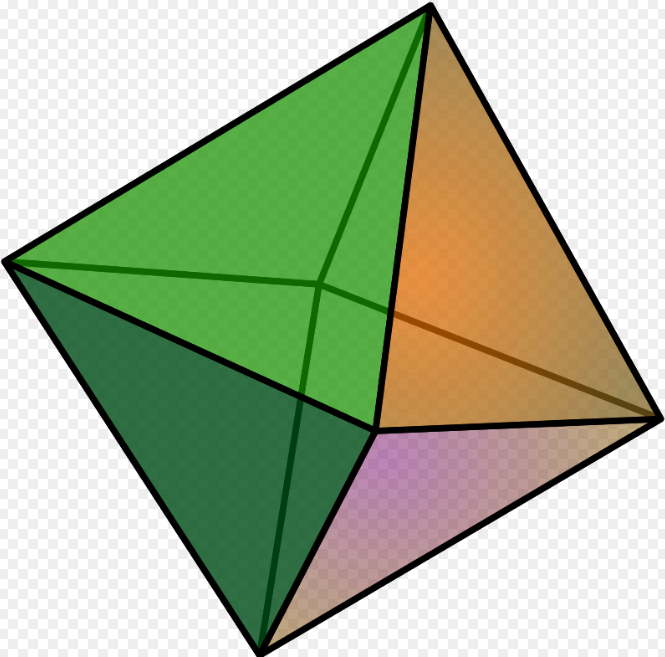
Hình bát diện đều vốn dĩ là nó là một phần của khối bát diện đều, và hình bát diện đều hiện nay cũng được định nghĩa là một khối bát diện đều được hình thành bởi nhiều những mặt hình bát diện đều với nhau. Cụ thể như là:
– Khối bát diện được chia ra thành hai khối đa diện đều lồi và khối đa diện lõm, khối bát diện được hình thành bởi những mặt đa giác bằng nhau và các cạnh bằng nhau.
– Và một khối bát diện đều không chỉ được hình thành bởi hình bát diện đều, vì hình bát diện đều cũng chỉ là một trong những phần của khối bát diện diện. Ngoài ra, thì trong khối bát diện đều còn có nhiều những phần khác như hình lập phương, hình 12 mặt đều, hình 20 mặt đều, hình tứ diện đều.
Bát diện đều có bao nhiêu mặt đối xứng
Nhìn chung và tổng thể của hình bát diện thì chúng ta có thể thấy, hình bát diện đều có cấu trúc được tạo thành bởi nhiều những hình đa giác có các cạnh bằng nhau. Vì thế, mà dựa vào một khối bát diện đều dưới đây, chúng ta có thể thấy bát diện đều có:
– Bát diện đều có 12 cạnh bằng nhau
– Bát diện đều có 6 đỉnh, được hình thành bởi những đỉnh của hình đa giác
– Bát diện có tổng cộng 8 mặt, mỗi mặt được tạo nên bởi các cạnh, đỉnh và mặt của hình đa giác
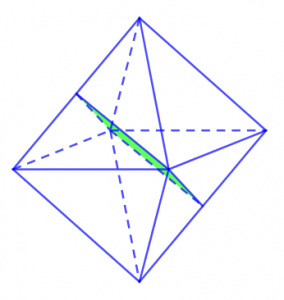
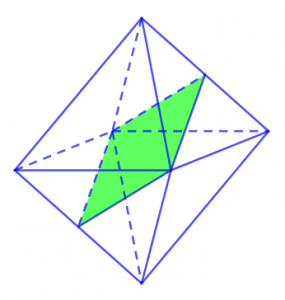
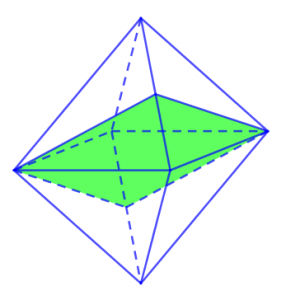
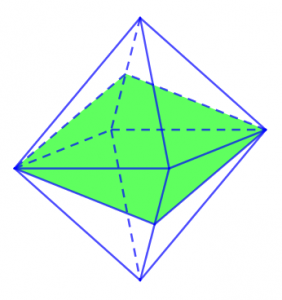
– Bát diện đều có 9 mặt phẳng đối xứng, 9 mặt phẳng đối xứng tương ứng với hai mặt hình đa giác đối diện với nhau.
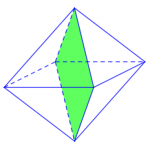
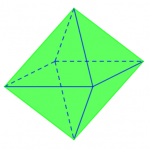
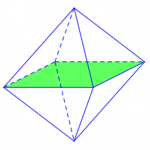
Trong số đó, thì khối bát diện hình thành nên 3 mặt phẳng đối xứng được tạo nên bởi sự chia cắt giữa các mặt phẳng đối xứng với nhau của 2 khối hình tứ giác đều có các cạnh bằng nhau. Còn riêng đối với 6 mặt phẳng đối xứng còn lại của bát diện thì được đi qua 2 đỉnh đối diện, hay còn gọi là một cặp đỉnh. Mỗi cặp đỉnh đối diện sẽ có tổng cộng 2 mặt phẳng đối diện, vậy ta kết luận được rằng 6 mặt phẳng đối diện còn lại của khối bát diện có tổng 3 đỉnh đối diện với 6 mặt phẳng đối diện.
Hình tứ giác đều có bao nhiêu mặt phẳng đối xứng
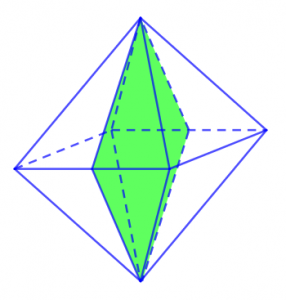
Hình tứ giác đều là một trong những phần tạo nên một khối bát diện đều hay còn gọi là hình bát diện đều. Và như vậy, chúng ta cũng sẽ tìm hiểu tương tự về số mặt phẳng đối xứng của một phần khối bát diện đều hình tứ giác đều nhé. Cũng tương tự như vậy, hình tứ giác đều hay còn được gọi là hình chóp tứ giác đều, tức là hình tứ giác có chung một điểm chóp với các đỉnh bằng nhau.
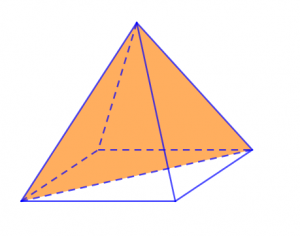
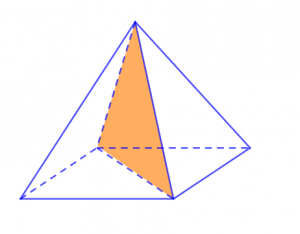
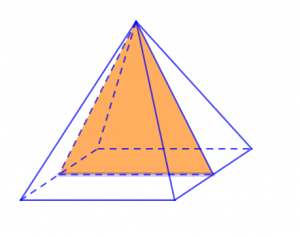
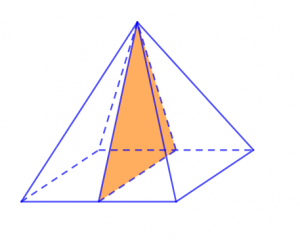
Và cũng tương tự như hình bát diện đều thì hình chóp tứ giác đều cũng được định nghĩa là khối chóp tứ giác đều. Khối chóp tứ giác đều có tổng cộng 4 mặt phẳng đối xứng, mỗi mặt phẳng đối xứng được hình thành bởi những hình tứ giác có đỉnh và những góc cạnh bằng nhau. Nếu như nhìn qua mô hình dưới đây thì những mặt phẳng đối xứng của hình chóp tứ giác đều khá giống với hình tam giác hơn.
Hình tứ diện đều có bao nhiêu mặt phẳng đối xứng
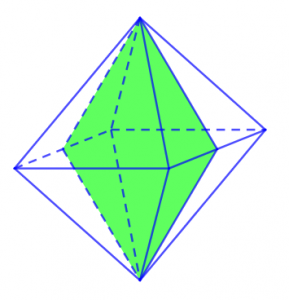
Cũng như hình chóp tứ giác đều thì hình tứ diện đều cũng là một trong những phần thuộc nằm trong của khối bát diện đều. Cũng tương tự như vậy thì ta có thể thấy được rằng, với một phần hình tứ diện đều nằm trong khối bát diện đều cũng sẽ có những mặt phẳng đối xứng như những phần hình khác nằm trong khối bát diện đều.
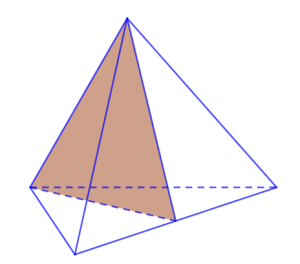
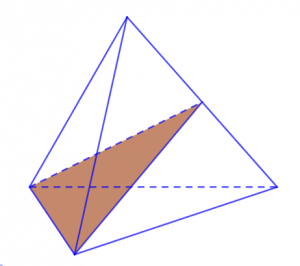
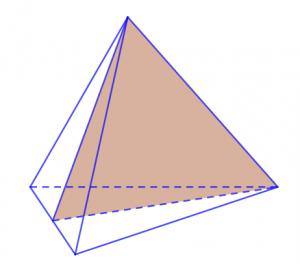
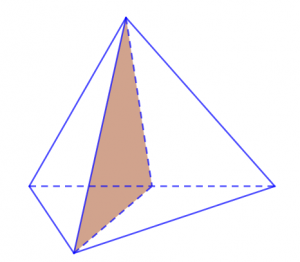
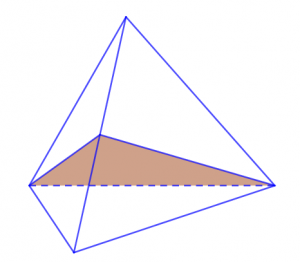
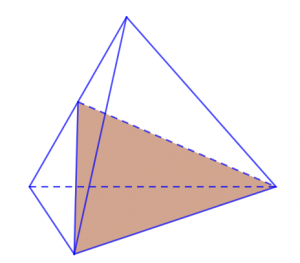
Khối tứ diện đều được hình thành bởi những mặt phẳng đối diện của những hình tam giác có góc nhọn, đỉnh và góc vuông bằng nhau. Nhìn vào mô hình chi tiết dưới đây thì ta có thể thấy được rằng khối tứ diện đều hay hình tứ diện đều có đến 6 mặt phẳng đối xứng. Những mặt phẳng đối xứng có chung một điểm giống nhau đó chính là chung đỉnh và khác nhau giữa các góc vuông hay góc nhọn của mỗi mặt đối xứng.
Hình lập phương có bao nhiêu mặt phẳng đối xứng
Hình lập phương hay còn được gọi là khối lập phương, và những mặt của khối lập phương được hình thành bởi những hình vuông có độ vuông góc là 90 độ. Hình lập phương là một trong những phần của khối bát diện đều, khối lập phương có tổng cộng 9 mặt phẳng đối xứng.
Trong đó, những mặt đối xứng của khối lập phương được chia thành 3 mặt phẳng đối xứng song song với 4 góc cạnh vuông góc của khối lập phương. Và với 3 mặt phẳng đối xứng này sẽ chia khối lập phương thành hai khối hình chữ nhật hay còn gọi là hai khối hộp.
Còn 6 mặt phẳng đối xứng còn lại của khối lập phương thì được chia thành 2 khối hình lăng trụ tam giác, được tiếp xúc với 4 cạnh vuông góc của khối lập phương. Và 6 mặt phẳng đối xứng còn lại của hình lập phương lại được chia ra thành hai khối lăng trụ hình tam giác như hình dưới đây. Điều này có thể thấy được rằng giữa các hình nằm trong khối bát diện đều có mối liên kết chặt chẽ với nhau.
Khối lăng trụ hình tam giác có bao nhiêu mặt phẳng đối xứng
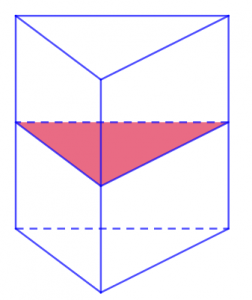
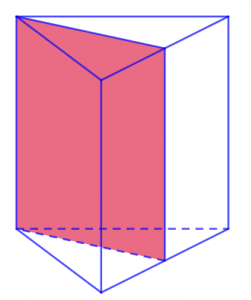
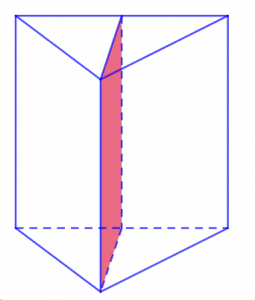
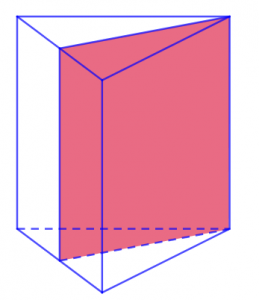
Riêng đối với khối lăng trụ hình tam giác thì sẽ có cách tính được mặt phẳng như sau: Số mặt phẳng đối xứng khối lăng trụ hình tam giác chính là bằng số trục khối lăng trụ đối xứng với mặt đáy + 1. Như vậy, một khối lăng trụ hình tam giác gồm có 3 trục đối xứng với mặt đáy + 1 mặt đáy. Ta kết luận được rằng khối lăng trụ hình tam giác có 4 mặt phẳng đối xứng.
Vậy thì qua bài viết Bát diện đều có bao nhiêu mặt phẳng đối xứng qua những chia sẻ ở trên thì bạn có thể thấy được rằng trong cấu trúc của khối bát diện đều còn có rất nhiều những cấu trúc với đa dạng hình để liên kết thành một khối bát diện hoàn chỉnh. Cảm ơn bạn đã thoe dõi bài viết, hãy cùng theo dõi baonhieu.net để biết thêm về những điều thú vị và những điều mà chúng ta vẫn còn chưa biết nhé.
